题目一：On Piecewise Sparse Signal Recovery

内容简介：In some applications, there are signals with piecewise sparse structure to be recovered. Suppose that a vector 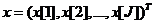 has 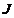 blocks, if each block  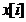is a sparse vector with support set 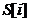, then we say  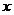is a piecewise sparse vector. Let 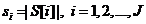, then  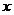is denoted by 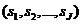-sparse vector. Denoted by 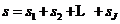, then  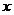is also a global 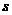-sparse vector. It needs to be pointed out that the piecewise sparse vector is quite different from the block sparse vector, which are well studied. In this talk, we will introduce some new results and algorithms on piecewise sparse signal recovery.

报告人：李崇君

报告人简介：大连理工大学数学科学学院教授、博士生导师，主要从事多元样条理论及应用方面的研究工作，涉及数值逼近，计算几何，有限元，微分方程数值解法等方向。在多元样条空间的维数稳定性及逼近理论方面获得一些研究成果，并发展了一类高精度的多元样条有限元方法。主持多项国家自然科学基金项目。2011年入选辽宁省“百千万人才工程”千人层次，2018年入选辽宁省高等学校创新人才，2018年获国家教学成果二等奖，2021年获全国优秀教材二等奖，2020年获宝钢优秀教师奖，2021年获评辽宁省本科教学名师，2023年入选“兴辽英才计划”教学名师，2015-2023年担任中国数学会计算数学分会委员，现任《计算数学》期刊编委、辽宁省数学会理事。

题目二：Solvable Dynamics of Coupled High-Dimensional Generalized Limit-Cycle Oscillators

内容简介：We introduce a new model consisting of globally coupled high-dimensional generalized limit-cycle oscillators, which explicitly incorporates the role of amplitude dynamics of individual units in the collective dynamics. In the limit of weak coupling, our model reduces to the D-dimensional Kuramoto phase model, akin to a similar classic construction of the well-known Kuramoto phase model from weakly coupled two-dimensional limit-cycle oscillators. For the practically important case of D = 3, the incoherence of the model is rigorously proved to be stable for negative coupling (K < 0) but unstable for positive coupling (K > 0); the locked states are shown to exist if K > 0; in particular, the onset of amplitude death is theoretically predicted. For D>=2, the discrete and continuous spectra for both locked states and amplitude death are governed by two general formulas. Our proposed D-dimensional model is physically more reasonable, because it is no longer constrained by fixed amplitude dynamics, which puts the recent studies of the D-dimensional Kuramoto phase model on a stronger footing by providing a more general framework for D-dimensional limit-cycle oscillators.

报告人：邹为

报告人简介：华南师范大学数学科学学院教授、博士生导师，广东省青年珠江学者，2010年获得中科院武汉物理与数学研究所应用数学博士学位，博士论文获2011年度中国科学院百篇优秀博士论文奖，2011年至2013年获得洪堡奖学金在德国柏林洪堡大学从事博士后研究工作，2016年至2018年在香港浸会大学从事香江学者博士后研究工作，长期从事复杂系统、非线性科学理论研究，在耦合非线性系统的集体动力学行为研究问题上取得一系列成果。目前已在非线性动力学主流学术期刊发表SCI论文50余篇，其中以第一并通讯作者发表2篇Physical Review Letters、1篇Nature Communications及1篇Physics Reports。目前主持1项国家自然科学基金面上项目，主持并完成国家自然科学基金2项。

时  间：2024年7月4日（周四）晚上20：00开始

地  点：腾讯会议790-182-994

热烈欢迎广大师生参加!

信息科学技术学院

2024年7月2日