近日，信息科学技术学院数学系、广东省数量金融大数据工程技术研究中心林义尊/王伟文/赖兆荣课题组撰写的两篇论文“Autonomous Sparse Mean-CVaR Portfolio Optimization”（论文一）和“Invariant Risk Minimization Is A Total Variation Model” （论文二）被机器学习领域的CCF A类国际顶级会议ICML2024录用。两篇论文均以暨南大学为唯一单位。论文一：数学系教师林义尊为第一作者、暨伯学院2023届本科毕业生张阳煜为第二作者、数学系教师赖兆荣为通讯作者兼第三作者、数学系2023级博士研究生李程为第四作者。论文二：赖兆荣为第一作者、数学系教师王伟文为通讯作者兼第二作者。

ICML的英文全称是International Conference on Machine Learning，中文官方名称为国际机器学习会议。它是机器学习领域两大国际顶级会议之一、中国计算机学会（CCF）推荐的A类会议之一，对论文的质量要求非常高。本届会议共收到9473篇投稿（不包括即时拒稿的论文），其中2609篇被录用，录用率约为27.5%。第41届ICML会议将于2024年7月21日至7月27日在奥地利维也纳举行。

论文一：

L0约束均值-条件在险价值模型是一种被广泛运用的既能精确控制选入资产数目、又能平衡收益与下行风险的资产组合优化模型。然而它的求解却是一个NP难问题，目前主流的求解方法往往采用计算成本高昂的组合策略。为了解决这一难题，本文提出了一种创新的自主稀疏均值-条件在险价值模型，它能够以任意所需的精度逼近原始的L0约束均值-条件在险价值模型。本文的方法核心在于将L0稀疏约束转化为指示函数（Indicator Function），并借助精心设计的尾部逼近函数（Tailed Approximation Function）来逼近这一指示函数。这一转变的巧妙之处在于，它将原本难以处理的单变量三项非凸优化模型转化为了更易于处理的双变量三项优化模型。进一步地，本文利用交替求解的策略，分别针对两个变量对应的双项非凸优化模型进行迭代求解，从而得到逼近模型的解。为了实现这一过程，本文开发了一个具有理论收敛性保证的近端交替线性化最小化算法（Proximal Alternating Linearized Minimization Algorithm）对自主稀疏均值-条件在险价值模型进行迭代求解。特别地，自主稀疏特性确保了在调整资产池大小时，大部分资产能够保持在所选资产池中，这与本文方法的初衷高度契合。总的来说，本文的方法不仅以理论上的保证对L0约束均值-条件在险价值模型进行了有效的逼近求解，还显著提高了计算效率，为资产配置问题提供了一个稳健且高效的解决方案。

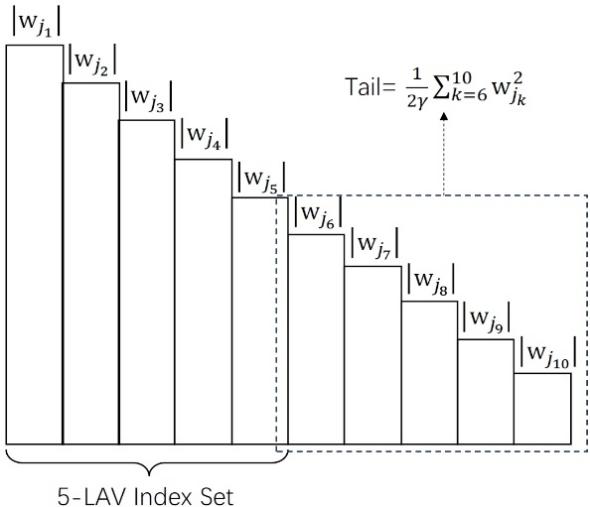
图一、L0约束的尾部逼近函数示意图（资产数量N取10，稀疏度m取5）：当资产组合策略w的L0范数大于m时，若γ趋于0，则尾部项（Tail）趋于正无穷，从而逼近原指示函数的取值。

论文二：

不变风险最小化准则是通用机器学习领域中的一种重要的分布外泛化手段。尽管关于该准则的很多不同设定以及不同应用场景被提出来，它的数学本质依然缺乏合理的解释。本文证明了在较为温和的条件下，该准则本质上是一个全变差-L2模型。在此基础上，本文提出一种基于全变差-L1模型的新的不变风险最小化框架。它不仅扩大了可被用作学习风险的函数类，还可利用余面积公式来保持不变特征，从而提高学习器对干扰特征的稳健性。文中还给出并证明了使得该框架实现分布外泛化的必要条件。在几种基准机器学习场景中的实验结果表明该框架取得了有竞争力的表现。

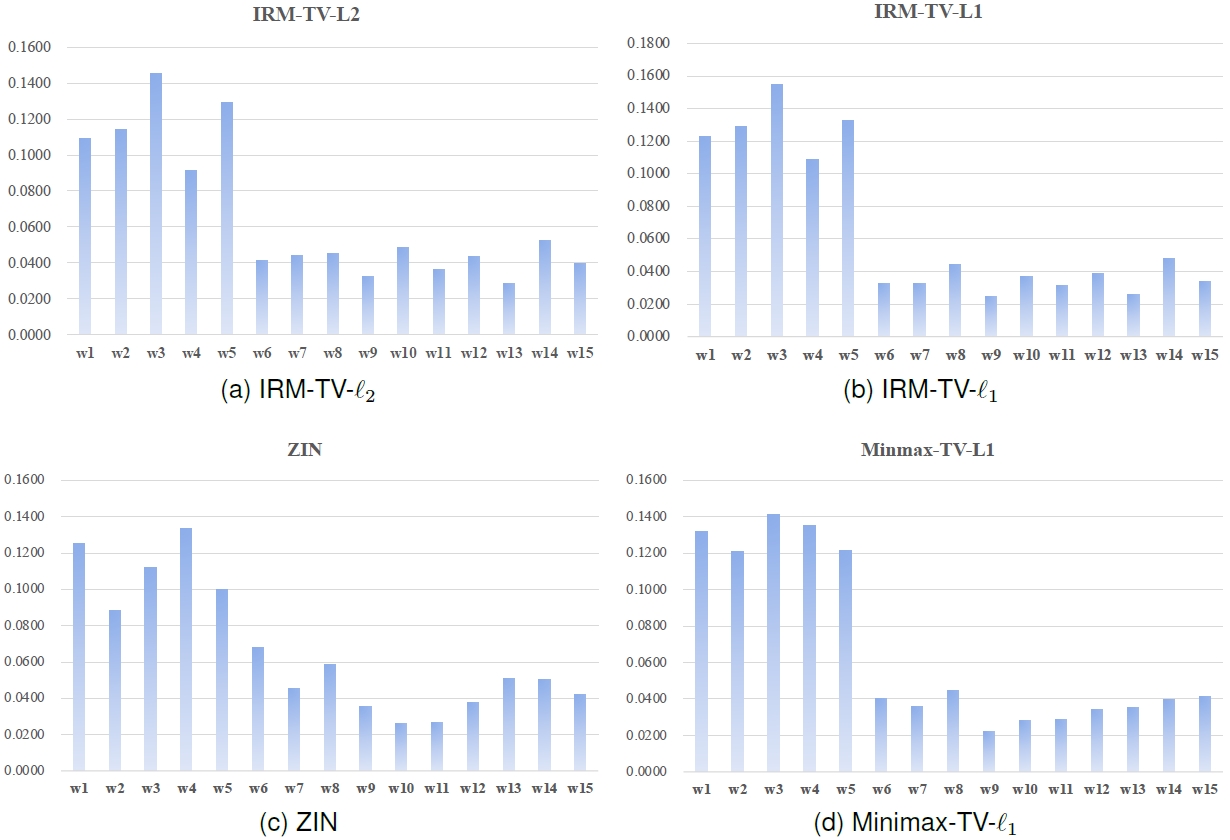
图二、不同方法所训练出来的特征权重占比。左边为基于全变差-L2模型的不变风险最小化方法，右边为基于全变差-L1模型的不变风险最小化方法。w1~w5对应不变特征，w6~w15对应干扰特征。可以看出右边的方法比左边的方法保持了更大占比的不变特征权重。

上述两篇论文成果依托于我校的广东省数量金融大数据工程技术研究中心，得到了国家自然科学基金面上项目（62176103）、广东省基础与应用基础研究基金项目（2021A1515110541）、广州市科技计划项目（2024A04J9896，2024A04J3940，2024A04J4225）、中央高校基本科研业务费（21623341）、广东省数量金融大数据工程技术研究中心运行费等项目的资助。文章的发表也表明我校和该工程中心的科研水平和青年教师的培养在高水平大学建设战略下得到显著提升。